| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- AI
- LSTM
- 선형대수
- Machine Learning
- DFS
- 딥러닝
- 머신러닝
- 이진 탐색
- 재귀함수
- GRU
- 퀵정렬
- 정렬
- 삽입정렬
- pytorch
- rnn
- 선택정렬
- 계수정렬
- 스택
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 큐
- 그리디
- 최단 경로
- BFS
- 알고리즘
- RESNET
- 다이나믹 프로그래밍
- 인공지능
- Today
- Total
hyeonzzz's Tech Blog
[파이토치 딥러닝 프로젝트 모음집] 1. 인공지능 본문
1.1 인공지능과 딥러닝
인공지능 : 인간의 학습, 추론, 지각 및 언어능력을 컴퓨터가 모방할 수 있도록 연구하고 구현하는 분야
- 인공지능 : 머신러닝과 딥러닝을 포함한 컴퓨터 과학, 전산학, 통계 및 개발 등 모든 관련 기술
- 머신러닝 : 정형 데이터를 활용한 인공지능 분야
- 딥러닝 : 비정형 데이터를 활용한 인공지능 분야
1.2.2 머신러닝 구분
- 지도학습 : 정답이 주어진 데이터를 활용하여 알고리즘을 통해 산출된 예측값과 정답을 비교하며 학습하는 방법
- 비지도학습 : 정답이 주어지지 않은 데이터를 탐색하여 패턴이나 내부 구조를 파악하는 학습 방법
- 강화학습 : 자신이 한 행동에 대한 보상을 받으며, 그 보상을 최대화할 수 있는 행동을 찾는 학습 방법
1.2.3 지도학습
지도학습
: 정답 혹은 레이블이 있는 환경에서 입출력 사이의 관계를 학습
- 정답을 비교하고 틀린 정도를 확인할 수 있다
- 알고리즘의 현재 상태를 평가할 수 있다
회귀 : 주가, 속도, 키와 같은 연속형 변수를 예측해야 하는 문제
분류 : 성별, 동물의 종류처럼 두 개 혹은 그 이상의 클래스로 분류하는 문제
손실함수
: 학습데이터 n개에 대한 예측 결과(ŷ)와 실제 정답(y) 사이의 차이
(얼마나 틀렸는지 채점하는 함수)
평균 제곱 오차(Mean Squared Error, MSE) : 예측값과 실제값의 유클리디안 거리를 측정 - 회귀에서 많이 사용

교차 엔트로피 오차(Cross Entropy Error, CEE) : 두 확률 분포의 차이를 측정 - 분류에서 많이 사용

지도학습 방법론
선형 회귀 모델
: y = f(X) + ε 의 형태로 출력변수(Y)와 입력 변수(X) 사이의 관계를 수학적 모형으로 추정
( ε : 외부 요인에 의해 생긴 잡음(Noise))

단순 선형 회귀 : 변수가 1개인 경우

다중 선형 회귀 : 변수가 여러개인 경우
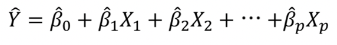
* 입력 변수가 많을수록 좋은 것은 아니다.
변수가 많을수록 과적합과 다중공선성 (입력 변수 사이에 높은 상관관계를 갖는 것)이 발생할 수 있다
- 회귀 계수가 불안정하게 추정된다
- 데이터의 작은 변화에도 민감하게 반응하게 된다
로지스틱 회귀 모델
: 출력값이 범주형인 경우 적용할 수 있는 회귀 모델

Odds : 임의의 사건이 실패할 확률 대비 성공할 확률의 비율

log 함수를 적용하여 범위를 -Inf ~ Inf로 변환한다. Log Odds의 형태를 시그모이드 함수라고 부른다.
로지스틱 회귀 모델 식

Lasso와 Ridge
- 일반화 : 일반화된 모델을 구성하는 기법
- 정규화 : 모델의 학습 Parameter를 추정하는 과정에서 Penalty Term 등을 추가하여 모델이 일반화를 도모하는 것
회귀 모델에 정규화를 적용한 방법론
: 손실 함수에 Penalty를 추가하여 회귀 계수가 과하게 추정되는 것을 막아준다

- λ : penalty의 영향력을 조절하는 하이퍼파라미처 (우리가 정함)
- Lasso는 L1-Penalty, Ridge는 L2-Penalty를 사용한다
- λ를 크게 설정하면, Penalty 부분의 회귀 계수를 줄여야 하므로 회귀 계수가 0에 가깝게 수렴된다
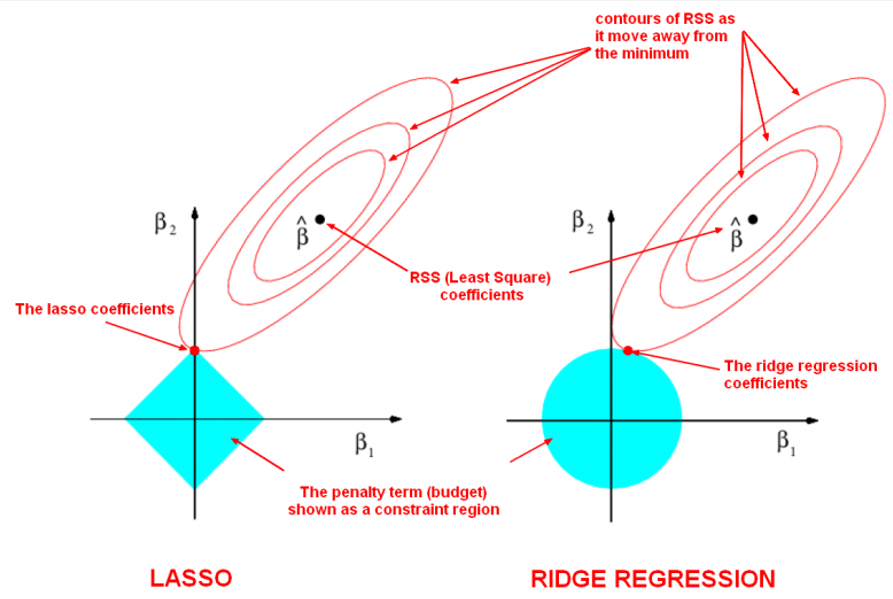
- 손실함수 + Penalty를 최소화하는 회귀 계수는 빨간 타원과 하늘색 음영이 맞닿는 부분이다
- Lasso는 상대적으로 중요하지 않은 변수의 회귀 계수를 0으로 만든다, 즉 전체 변수 중 일부 변수만을 선택한다
- Ridge는 0에 가까운 작은 수로 축소시킨다, 즉 전체적으로 0에 가까운 회귀 계수로 감소시킨다
의사결정 나무 (Decision Tree)
: 입력 변수를 조합한 규칙으로 출력 변수를 예측하는 모델

- 스무고개처럼 예, 아니요로만 대답한다
- 정답의 후보를 줄여가며 최종 정답을 찾아낸다
- 단일 모델로 사용하기에는 예측 성능이 낮다
Support Vector Machine (SVM)
: 클래스를 가장 잘 나눌 수 있는 결정 경계 (Decision Boundary)를 정하는 모델

- Support Vector : 각 클래스에서 결정 경계와 가장 가까운 데이터
- Margin : 두 클래스 사이의 거리
- 초평면 (Hyperplane) : Margin을 최대화하는 결정 경계
- 초평면을 찾는 것이 SVM의 목적이다
k-Nearest Neighbors (k-NN)
: 새로운 데이터가 입력되었을 때, 가장 가까운 데이터 k개를 이용하여 해당 데이터를 유추하는 모델
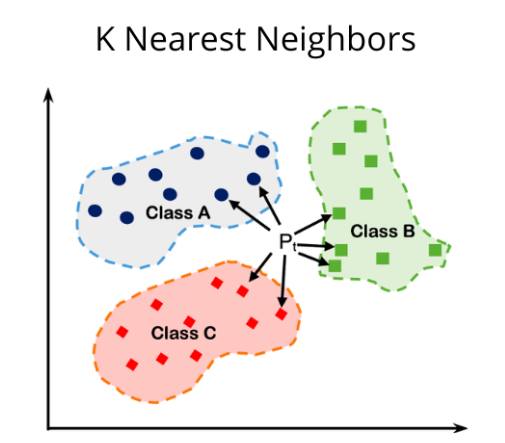
- 새로운 데이터를 가장 가까운 데이터 7개를 고려하여 예측하였다
- 거리를 모두 계산하고 비교해야 하므로 데이터가 많을수록 학습 속도가 급격하게 느려진다
- k : 이웃의 수 (우리가 결정)
- k가 너무 작으면 시야가 좁아져 과적합의 가능성이 있고, k가 너무 크면 주변 데이터를 고려하는 의미가 사라진다
앙상블 모형 (Ensemble Model)
: 여러 모형의 결과를 종합하여 단일 모형보다 정확도를 높이는 방법

- '표본 추출 + 모델링' 과정을 여러 번 반복하여 진행된다
- 반복 모델링한 여러 결괏값을 회귀는 평균, 분류는 투표를 통해 최종 예측값을 결정한다
배깅
: 이미 존재하는 데이터로부터 같은 크기의 표본을 여러 번 복원추출한 Boostrap Sample에 대해 예측 모델을 생성한 후 그 결과를 조합
부스팅
: Boostrap Sample을 구성하는 과정에서 이전 모델의 결과를 반영하여 잘못 예측된 데이터의 비율을 높여 더욱 집중적으로 학습하는 방법론
랜덤 포레스트
: 배깅의 일종으로 각 의사결정 나무 모델링 단계에서 변수를 랜덤으로 선택하여 진행하는 방법론
1.2.4 비지도학습
비지도학습
: 정답 혹은 레이블이 주어지지 않은 상태에서의 학습 방법
군집화 (Clustering)
: 특징이 유사한 데이터끼리 묶어 여러 개의 군집으로 나누는 방법
군집 과정
- 군집 내 응집도 최대화 : 동일한 군집에 소속된 개체들은 서로 유사할수록 좋음
- 군집 간 분리도 최대화 : 상이한 군집에 소속된 개체들은 서로 다를수록 좋음
차원 축소 (Dimensionality Reduction)
: 고차원의 데이터를 저차원의 데이터로 축소하는 방법
- 변수 선택 : 갖고 있는 변수 중에서 일부 변수만 선택하여 학습에 사용
- 변수 추출 : 변수를 조합하여 새로운 변수로 재창조
1.2.5 과적합과 모델 학습법
과적합이 발생하는 이유
- 데이터 수가 적은 경우 - Data Augmentation으로 극복
- 입력 변수의 개수가 많은 경우 - 입력 변수의 수를 줄이는 차원 축소 기법
- 복잡한 모델을 사용한 경우 - Penalty를 통한 Regularization
데이터셋
- Training Data : 모델을 학습시키기 위한 데이터
- Validation Data : 학습 데이터로 학습된 모델을 검증 데이터에 적용하여 정확도를 확인. 과적합 판단, Hyperparameter 선택
- Test Data : 최종적으로 결정된 모델의 성능을 측정하는 데이터
검증 데이터 - 정답을 알고 있다는 가정하에 사용
테스트 데이터 - 정답을 모르는 상태임을 가정
주로 7:2:1 또는 6:2:2 비율로 구성
과적합된 상황을 알 수 있는 방법
: test data에서 오히려 예측력이 떨어진다
1.2.6 성능 지표
손실 함수와 성능 지표는 수식이 같은 경우가 많다
손실 함수 : 모델을 학습시킬 때 방향성을 제공한다. 학습 Parameter를 추정하는 데 영향을 준다
성능 지표 : 학습이 완료된 모델의 성능을 평가한다. 검증 및 테스트 데이터로 측정하고 모니터링하는 수단. 모델에는 어떠한 영향도 미치지 않는다
회귀의 성능 지표
MSE

MAPE (Mean Absolute Percentage Error)
: 실제값 대비 오차의 정도를 퍼센트값으로 나타낸다

분류의 성능 지표
: Confusion Matrix의 형태로 모델 성능을 판단한다

- 정확도 (Accuracy) : 모델이 올바르게 분류한 비율
- 정밀도 (Precision) : 예측값이 Positive라 분류된 것 중 실제값이 Positive인 비율
- 재현도 (Recall) : 실제값이 Positive인 것 중 예측값이 Positive라 분류된 비율
- F1 Score : 정밀도와 재현도의 조화평균

분류 문제에서는 각 클래스가 갖는 데이터량의 차이가 큰 경우 데이터 불균형 문제가 발생한다.
예를 들어 100개의 거래 내역 중 99개가 정상 거래, 1개가 금융 사기 거래일 때, 예측값 100개가 모두 정상 거래로 판정된다면 해당 모형은 99%의 정확도를 갖는다. 하지만 정밀도는 0%의 성능을 갖는다.
'Deep Learning > Basics' 카테고리의 다른 글
| [Andrew Ng] 딥러닝 4단계 : 2. 케이스 스터디 (1) | 2024.06.10 |
|---|---|
| seq2seq, Attention, Transformer, BERT 정리 (0) | 2024.05.31 |
| 순환 신경망 - LSTM / GRU (0) | 2024.03.08 |
| [Andrew Ng] 딥러닝 4단계 : 1. 합성곱 신경망 네트워크 (CNN) (0) | 2024.02.05 |
| [Andrew Ng] 딥러닝 2단계 : 7. 다중 클래스 분류 (2) | 2024.02.01 |



