| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- BFS
- Machine Learning
- 퀵정렬
- 큐
- 정렬
- 재귀함수
- 머신러닝
- 알고리즘
- 스택
- 인공지능
- DFS
- RESNET
- pytorch
- 선형대수
- 삽입정렬
- 딥러닝
- 최단 경로
- 계수정렬
- 선택정렬
- 다이나믹 프로그래밍
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- LSTM
- 이진 탐색
- 그리디
- GRU
- AI
- rnn
- Today
- Total
hyeonzzz's Tech Blog
[인공지능을 위한 선형대수] 3. Least Square - 정규방정식 본문
정규방정식

x^ : 최단거리의 수선의 발을 만들어내게 하는 선형 결합의 계수
normal equation : 최단거리의 수선의 발을 만들어내기 위해 만족하는 식

위 식과 동일하지만 방정식을 푸는 문제로 바꾼다

A^TA 가 invertible할 때(역행렬이 존재할 때)와 invertible하지 않을 때 두가지로 나누어 볼 수 있다
1) invertible한 경우
x^ = ( A^TA )-1 A^T b 의 식으로 나타낼 수 있다
+) 복습
역행렬은 정사각행렬에서만 논할 수 있다. 따라서 A의 사이즈가 100 x 3이고 A^T 의 사이즈가 3 x 100 이라면 A^TA 의 사이즈는 3 x 3 이 된다. 즉, feature 갯수 만큼의 정사각행렬이다.

* 다른 방식으로의 유도
b - Ax 를 최소화하기 위한 x값을 찾는 것 = 제곱을 했을 때 값을 최소화하기 위한 x값을 찾는 것

위 식을 사용하여 식을 변형할 수 있다.

값을 계산하면 scalar 값이 된다
최소값을 찾기 위해 x에 대해 미분하면 상수값은 없어지고 x는 벡터형의 변수이므로 다음과 같이 계산된다.
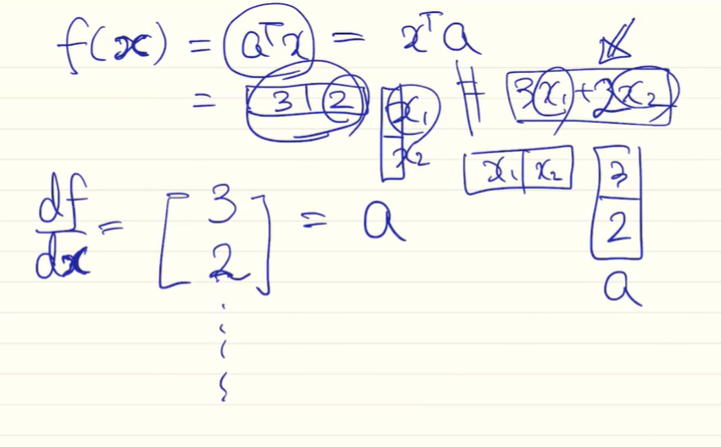
편미분된 벡터는 column 벡터 a 와 같다. 따라서 f(x) = a^T x = x^T a 이다.
이것을 이용해 x^T A^T b 를 x에 대해 미분해보면

A^T b 를 먼저 계산해 column 벡터를 얻고 이 column 벡터는 위의 a와 같은 역할이므로
x^T A^T b 를 미분하면 A^T b 이다.
마찬가지로 (b^T A) x = x^T (b^T A)^T 이므로 미분하면 A^T b 이다.
x^T A^T Ax 는 합성함수의 미분으로 볼 수 있다.

이를 이용해 계산하면
(x^T를 변수로 보고 미분한 것)

+ (x를 변수로 보고 미분한 것)
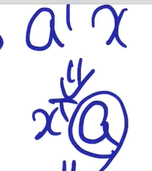


이므로 normal equation의 수식과 같음을 확인할 수 있다
2) invertible하지 않은 경우

해는 무수히 많다. (해가 없는 경우는 없다)
왜 해가 없는 경우는 없는가?
-> b^이 없는 경우, 즉 수선의 발이 없는 경우는 없다
언제 역행렬이 존재하지 않는가?
-> matrix A의 column vector들이 선형 의존인 경우
수선의 발은 unique하다. 따라서 b^은 한 점이고 b^을 만들기 위한 평행사변형은 무수히 많다
+) 하지만 A^T A의 역행렬이 존재하지 않는 경우는 거의 없다
-> dimension이 커질수록 feature값이 벗어나는 경우가 많기 때문이다

'Mathematics > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 3. Least Square - Orthogonal Projection Ⅱ (0) | 2024.03.27 |
|---|---|
| [인공지능을 위한 선형대수] 3. Least Square - Orthogonal Projection Ⅰ (0) | 2024.03.27 |
| [인공지능을 위한 선형대수] 3. Least Square - Least Squares와 그 기하학적 의미 (0) | 2024.03.26 |
| [인공지능을 위한 선형대수] 3. Least Square - Least Squares Problem 소개 (0) | 2024.03.26 |
| [인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 전사함수와 일대일함수 (0) | 2024.03.25 |




