| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- BFS
- 그리디
- RESNET
- 최단 경로
- 인공지능
- 스택
- 선택정렬
- 알고리즘
- GRU
- 머신러닝
- pytorch
- rnn
- 이진 탐색
- 재귀함수
- 삽입정렬
- AI
- 선형대수
- 퀵정렬
- 큐
- LSTM
- 계수정렬
- Machine Learning
- DFS
- 다이나믹 프로그래밍
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 딥러닝
- 정렬
- Today
- Total
hyeonzzz's Tech Blog
[인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 선형변환 with Neural Networks 본문
[인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 선형변환 with Neural Networks
hyeonzzz 2024. 3. 25. 20:18선형변환 with Neural Networks

2차원에서 2차원으로 변환되는 layer라고 생각했을 때 (bias 없음)
matrix A = coefficient들의 집합



기저벡터에 각각 2배, 1배로 길이를 늘려주고 줄여줘서 좌표값을 만든 것이다
여기서 선형 변환의 의미는 [1, 0], [0, 1]이 변환되고 난 벡터에 coefficient를 나중에 적용해서 만들어진 벡터가 최종 output이다.

예를 들어 (2,1)이라는 입력 벡터가 주어졌을 때 (1, 0)은 2배가 되고 (0, 1)은 1배가 된다. 애초에 (2,1)이 갖고 있는 coefficient는 2였기 때문에 기울어진 초록색선 (2,3)이 2배가 되어 (4,6)이 된다. (0,1)은 1이었기 때문에 그대로 (1,4)가 된다.
즉, 좌표값을 dispersion(분산)시켜서 정사각형을 기울어진 평행사변형으로 만들어준다.
기저벡터가 변환된 output으로 다시 모눈종이를 그릴 수 있다.

이것이 선형 변환에서 일어나는 일이다
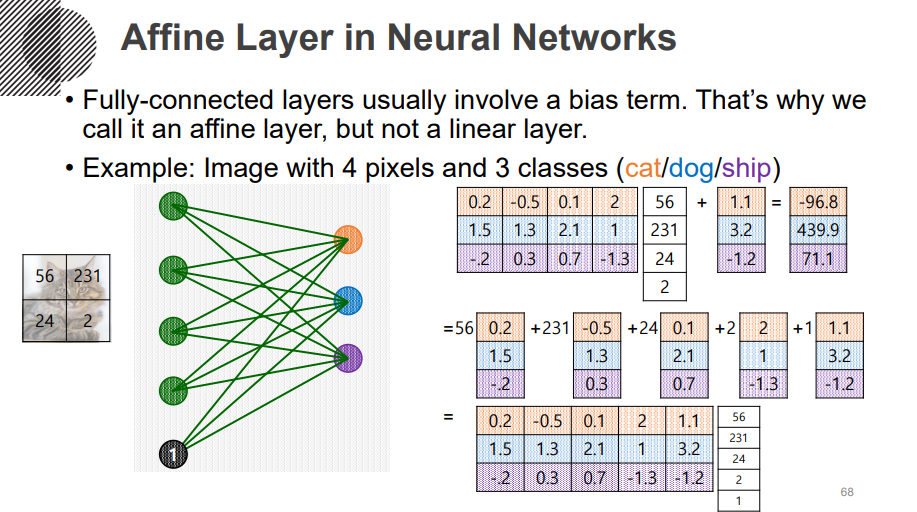
픽셀 4개로 이루어진 이미지가 있다고 했을 때 4개의 dimension을 가지는 input layer가 된다. 1은 bias term이다.
입력 벡터를 3차원으로 만들어주는 선형 변환에 해당하는 matrix가 주어지고 학습에 의해 최적화가 된다. 그 옆엔 bias에 의해 넘어오는 상수 벡터가 더해진다. 출력 결과에 sigmoid나 ReLU를 걸어 최종적인 non-linear unit을 통과하고 최종적인 output이 나온다. 이렇게 상수가 껴있으면 affine transformation 라고 부른다. bias term이 존재하는 경우에도 하나의 선형 변환으로 만들 수 있다.
-> column combination 사용

input으로 들어오는 feature 벡터에 1을 끼워넣고 선형 변환을 통해 bias term을 해결한다.

fully connected layer을 column들의 combination으로 생각한다면
노드의 값은 각 병에 걸릴 score 값을 만들어주는 것이므로 키가 1이라면 각 병에 0.2, 1.5, -0.2의 확률을 보내주는 것이다. 몸무게는 각 병에 -0.5, 1.3, 0.3의 확률을 보내준다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 3. Least Square - Least Squares Problem 소개 (0) | 2024.03.26 |
|---|---|
| [인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 전사함수와 일대일함수 (0) | 2024.03.25 |
| [인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 선형변환 (1) | 2024.03.25 |
| [인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 부분공간의 기저와 차원 (0) | 2024.03.25 |
| [인공지능을 위한 선형대수] 2. 선형시스템 및 선형변환 - 선형독립과 선형종속 (0) | 2024.03.25 |




