| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 삽입정렬
- 퀵정렬
- 머신러닝
- 선택정렬
- 최단 경로
- RESNET
- 알고리즘
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- pytorch
- Machine Learning
- 딥러닝
- DFS
- 계수정렬
- AI
- 이진 탐색
- 스택
- 선형대수
- 재귀함수
- 인공지능
- BFS
- 정렬
- 다이나믹 프로그래밍
- GRU
- 그리디
- rnn
- LSTM
- 큐
- Today
- Total
hyeonzzz's Tech Blog
[인공지능을 위한 선형대수] 3. Least Square - 그람-슈미트 직교화와 QR 분해 본문
[인공지능을 위한 선형대수] 3. Least Square - 그람-슈미트 직교화와 QR 분해
hyeonzzz 2024. 3. 27. 19:00그람-슈미트 직교화와 QR 분해
벡터들을 서로 수직이 되도록 하여 서로에게 영향을 주지 않도록 한다

x1과 x2는 내적을 했을 때 0이 아니므로 수직이 아니다.
두 벡터가 수직이고 길이가 1이 되도록 만드려면 어떻게 해야할까?

v1을 길이가 1이 되도록 만든다

v2를 u1 위에 projection 시켜 만든 벡터를 v2에서 뺀다 - 초록색 벡터(u2)만 남는다

1. v2와 u1을 내적시킨다 - 길이를 찾은 것


2. v2 - (길이) * (방향)

3. 길이를 1로 만든다
세번째 벡터가 추가로 주어졌다면?

1. 첫번째 벡터에 projection 시킨다
2. 두번째 벡터에 projection 시킨다
3. 원래 벡터에서 둘을 뺀다
4. 길이가 1이 되도록 한다
부가적인 matrix를 추가해 원래 벡터 복원하기

새로운 matrix가 가중치 역할을 해서 가운데 벡터에 곱해져 선형결합한 형태가 원래 벡터가 되어야 한다.

1. 첫번째 벡터는 normalize한 것 뿐이기 때문에 나눈 값을 쓴다

2. 두번째 벡터는 초록색 두 벡터의 linear combination을 이용한다
[0, 0, 2]를 구한 과정을 생각해보면 (원래 벡터 [1, 2, 2]) - (projection된 길이 )* (u1방향성) 를 normalize 했다

따라서 [1, 2, 2]를 구하기 위해서는 [0, 0, 2] + (projection된 길이 )* (u1방향성)을 하면 된다
결국 (projection된 길이 )는 (u1방향성)벡터의 선형 결합에 쓰이는 가중치가 된다.
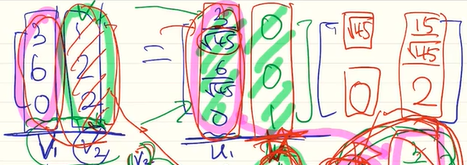
따라서 위에는 첫번째 벡터와 곱해지는 가중치를 쓰고 / 밑에는 normalize하는데 나눠준 수를 쓴다
정리

1. normalization 한 값을 쓴다

2. 첫번째 열 coefficient(계수)
맨위 - normalization coefficient
나머지는 쓰지 않아도 되므로 0으로 채운다

3. 두번째 열 coefficient(계수)
맨위 - 연두색 벡터에 projection된 벡터의 길이
아래 - 길이를 1로 만들어주는데 쓴 값
나머지는 쓰지 않아도 되므로 0으로 채운다

matrix A는 두개로 분해가 된다.
matrix A - linearly independent 한 column 들
matrix Q - 동일한 column 수를 갖되 orthonomal 한 basis 들
matrix R - triangle한 matrix
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 3. Least Square - Orthogonal Projection Ⅱ (0) | 2024.03.27 |
|---|---|
| [인공지능을 위한 선형대수] 3. Least Square - Orthogonal Projection Ⅰ (0) | 2024.03.27 |
| [인공지능을 위한 선형대수] 3. Least Square - 정규방정식 (0) | 2024.03.27 |
| [인공지능을 위한 선형대수] 3. Least Square - Least Squares와 그 기하학적 의미 (0) | 2024.03.26 |
| [인공지능을 위한 선형대수] 3. Least Square - Least Squares Problem 소개 (0) | 2024.03.26 |




