| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 큐
- 최단 경로
- pytorch
- DFS
- rnn
- RESNET
- 머신러닝
- 딥러닝
- Machine Learning
- 정렬
- 그리디
- 재귀함수
- 선택정렬
- 인공지능
- BFS
- 선형대수
- LSTM
- 알고리즘
- AI
- 스택
- GRU
- 삽입정렬
- 이진 탐색
- 퀵정렬
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 계수정렬
- 다이나믹 프로그래밍
- Today
- Total
hyeonzzz's Tech Blog
[Andrew Ng] 딥러닝 2단계 : 5. 하이퍼파라미터 튜닝 본문
1. 튜닝 프로세스

심층신경망에서 다뤄야 할 하이퍼파라미터
1. 학습률 α
2. 모멘텀 알고리즘의 β, Adam 최적화 알고리즘의 β1, β2, ε
3. 층의 수
4. 층에서 은닉 유닛의 수
5. 학습률 감쇠 정도
6. 미니 배치의 크기
학습률 α는 튜닝해야 할 가장 중요한 하이퍼파라미터이고요. α 이외에 주로 튜닝하는 것들로는 모멘텀이 있겠고, 기본값 0.9 정도로 설정할 수 있겠고요. 최적화 알고리즘을 효율적으로 돌리기 위해 미니 배치 크기도 튜닝할 수 있습니다. 은닉 유닛도 자주 튜닝합니다.
여기 오렌지색 박스는 학습률 α 다음으로 중요한 것들이고요. 층의 숫자도 큰 차이를 만들 수 있고, 학습률 감쇠도 마찬가지입니다. 그리고 Adam 알고리즘에서는 β1, β2, ε는 튜닝을 하지 않고 0.9, 0.999, 10^(-8)을 항상 사용합니다. 물론 원한다면 튜닝을 해도 좋습니다.
당연히 α가 가장 중요하고요. 다음으로 오렌지색 박스, 그 뒤를 이어 보라색 박스 순입니다. 그러나 딱 정해진 것은 아닙니다. 어떤 전문가들은 동의하지 않거나 다른 직관을 갖고 있을 수도 있지요.

만약 하이퍼파라미터를 튜닝한다면 어떤 값을 탐색할지 어떻게 정할 수 있을까요?
머신러닝이 만들어진지 얼마 되지 않았을 때는 두 개의 하이퍼파라미터가 있을 때 각각 Hyperparameter1 Hyperparameter2라고 부를 건데요. 격자점을 탐색하는 것이 일반적이었습니다. 이렇게 말이죠. 그리고 체계적으로 여기 있는 값들을 탐색하는 것이지요. 실제로는 더 크거나 작을 수도 있겠지만 여기서는 5X5 격자에서 25개의 점만 생각하죠. 그리고 최고의 하이퍼파라미터를 정하는 겁니다. 이 예시는 하이퍼파라미터의 수가 적을 때 쓸 수 있습니다.
하지만 딥러닝에서는 이런 방식을 추천드립니다. 무작위로 점들을 선택하는 것이지요. 동일하게 25개의 점만 생각해볼까요? 그 점들에 대해서 하이퍼파라미터를 정하는 겁니다. 이렇게 하는 이유는 어떤 하이퍼파라미터가 문제 해결에 더 중요한지 미리 알 수 없기 때문입니다. 이전 슬라이드에서 보신 것처럼 하이퍼파라미터의 중요도 순위가 있습니다. 예를 들어 Hyperparameter1이 학습속도 α이고 극단적인 경우로 Hyperparameter2를 ε라고 합시다. Adam 알고리즘에서 분모에 있는 값 말이죠. 이런 경우 α를 고르는 것이 ε을 고르는 것보다 더 중요합니다. 그래서 격자점으로 다시 돌아가면 5개의 α 값을 확인하게 되는데 이때 ε 값이 달라도 결과는 같은 것을 확인할 수 있을 겁니다. 25개의 모델을 학습시켰지만 가장 중요한 하이퍼파라미터인 α 5개에 대해서만 학습시킨 것과 다를 게 없죠.
반대로 무작위로 모델을 고르면 어떨까요? 그러면 아시다시피 25개의 서로 다른 학습속도 α 값을 이용하여 학습시키게 되고 더 좋은 하이퍼파라미터를 잘 찾게 될 겁니다. 여기서는 두 개의 하이퍼파라미터만 써서 예를 들었는데요. 실제로는 훨씬 많은 하이퍼파라미터를 다루게 될 겁니다. 예컨대 세 개의 하이퍼파라미터를 다룬다고 하면 정사각형을 탐색하는 것이 아니라 정육면체를 탐색하는 것이죠. 그리고 세 번째 차원은 Hyperparameter3을 가리킬 거고요. 이 3차원 정육면체 안에서 모델을 고른다면 각 하이퍼파라미터에 대해서 훨씬 많은 값을 시험해보게 될 겁니다. 실제로는 3보다 더 많은 하이퍼파라미터를 탐색하곤 합니다.

다른 일반적인 방법 중 하나는 정밀화 접근입니다.
여기 2차원 예시에서 이 점들을 사용한다고 해보죠. 그리고 이 점이 최고라는 걸 찾았습니다. 아마 그 주변에 있는 점들도 좋은 성능을 보이겠죠? 그러면 정밀화 접근에서는 이렇게 더 작은 영역으로 확대해서 더 조밀하게 점들을 선택합니다. 무작위인 것은 그대로이지만, 최고의 하이퍼파라미터들이 이 영역에 있으리라는 믿음 하에 파란색 사각형 안에 초점을 두고 탐색하는 것이죠. 즉, 전체 사각형에서 탐색한 뒤에 더 작은 사각형으로 범위를 좁혀나가는 겁니다. 그러면 여기에서 더 조밀하게 시험해볼 수 있겠죠.
2. 적절한 척도 선택하기

지난 비디오에서는 무작위로 하이퍼파라미터를 찾는 것이 더 효율적인 탐색이라는 것을 배웠습니다. 하지만 여기서 무작위라는 것이 가능한 값들 중 공평하게 뽑는 것이라고 할 수는 없습니다. 대신 적절한 척도를 정하는 것이 더욱 중요합니다. 이 영상에서는 어떻게 척도를 정하는지 알아보겠습니다.
어떤 레이어 l에 대해서 은닉 유닛의 수 n^l을 정한다고 합시다. 그리고 값의 범위로 50부터 100을 생각해보죠. 이런 경우 50부터 100까지의 수직선에서 무작위하게 값들을 고른다고 합시다. 하이퍼파라미터를 고르는 꽤 합리적인 방법이지요. 또는 신경망에서 레이어의 숫자 L을 정한다고 했을 때 층의 숫자가 2에서 4 사이라고 생각할 수 있겠죠. 2에서 4까지의 숫자를 선택할 때 무작위하게 뽑는 것은 물론이거니와 격자점을 사용해도 문제가 없습니다. 이 예시들은 가능한 값 중 무작위하게 뽑는 것이 합리적인 경우들입니다.

다른 예시들을 살펴봅시다.
학습률 α를 탐색하는데 범위로 0.0001부터 1까지를 생각하고 있다고 합시다. 0.0001에서 1까지의 수직선 상에서 균일하게 무작위로 값을 고르겠죠. 여기서 약 90%의 샘플이 0.1과 1 사이에 있을 겁니다. 즉 90%의 자원을 0.1과 1 사이를 탐색하는 데 쓰고 단 10%만을 0.0001과 0.1 사이를 탐색하는 데 쓰는 것이죠. 비합리적이지 않나요?
대신 선형 척도 대신 로그 척도에서 하이퍼파라미터를 찾는 것이 더 합리적입니다. 수직선 위에 0.0001부터 0.001, 0.01까지 값들이 있겠죠? 0.1과 1도 있을 테고요. 이런 로그 척도에서 균일하게 무작위로 값을 뽑는 겁니다. 그러면 0.0001과 0.001 사이, 0.001과 0.01 사이를 탐색할 때 더 많은 자원을 쓸 수 있는 것이지요.
파이썬에서는 어떻게 구현할 수 있을까요? r = -4 * np.random.rand()를 쓰고요. 그러면 무작위로 선택된 α 값은 10^r이 되겠죠. 이 첫 번째 줄에서 r은 -4와 0 사이의 무작위 값일테고 α 값은 따라서 10^-4와 10^0 사이, 즉 10^-4와 1 사이가 되겠지요.
더 일반적인 경우를 볼까요? 10^a에서 10^b까지를 로그 척도로 탐색한다면 이 예시에서는 0.0001이 10^a가 되겠죠? 따라서 a는 10을 밑으로 하는 log를 0.0001에 대해 취하면 얻을 수 있습니다. 그 결과 a가 -4가 될 테고요. 마찬가지로 오른쪽 값도 10^b가 되겠죠. 여기서 b는 10이 밑인 log를 1에 취하면 0이라는 것을 알 수 있습니다. 그리고 어떻게 하죠? r은 a와 b사이서 균일하게 무작위로 뽑히고요. 이 경우 r은 -4와 0 사이겠죠? 그리고 무작위의 하이퍼파라미터 α는 10^r이 되겠습니다.
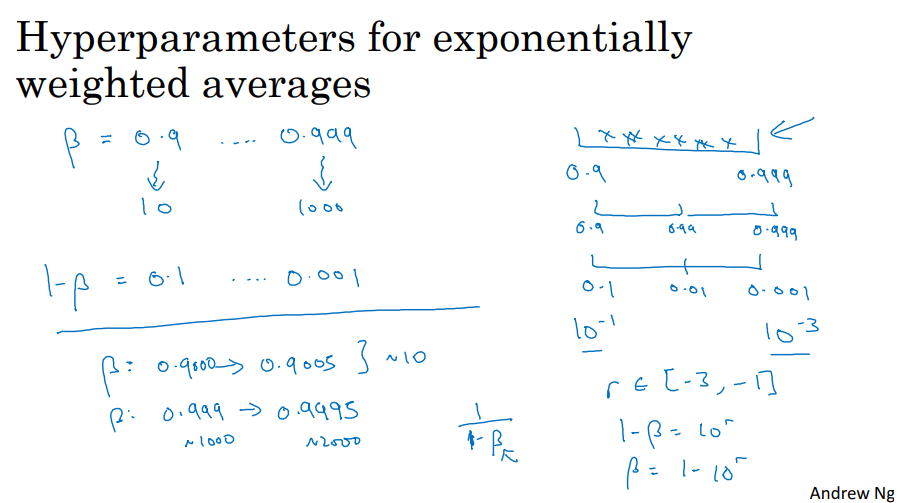
또다른 예시는 지수가중평균을 계산할 때 사용되는 하이퍼파라미터 β에 관한 것인데요.
β를 0.9와 0.999 사이에서 찾는다고 합시다. 이 범위를 탐색하는 것이지요. 0.9의 경우에는 지수가중평균이 최근 10일의 평균 기온처럼 마지막 10개 값의 평균과 비슷하고, 0.999의 경우에는 마지막 1000개 값의 평균과 비슷했던 것 기억하시나요? 방금 전 슬라이드에서 봤던 것처럼 만약 0.9와 0.999 사이를 탐색한다면 0.9와 0.999 사이를 균일하게 무작위 탐색하는 것은 합리적이지 않습니다. 더 나은 방법은 1-β에 대해서 값을 탐색하는 것이지요. 그러면 0.1부터 0.001이 되겠죠? 그러면 β를 0.1에서 0.01을 거쳐 0.001사이에서 탐색하는 겁니다. 지난 슬라이드에서 봤던 방법을 써보자면 0.1은 10^-1이고, 0.001 10^-3입니다. 이전 슬라이드에서는 작은 값이 왼쪽 큰 값이 오른쪽에 있었지만 여기서는 반대입니다. 큰 값이 왼쪽, 작은 값이 오른쪽에 있죠. 즉 여기서 해야 할 일은 -3과 -1 사이에서 균일하게 무작위로 값을 뽑는 겁니다. 이제 1-β를 10^r로 생각하면 되니 β가 1-10^r이 되겠죠. 이렇게 적절한 척도 위에서 무작위로 하이퍼파라미터 샘플을 추출했습니다. 이 방법을 이용하면 0.9부터 0.99를 탐색할 때와 0.99부터 0.999를 탐색할 때 동일한 양의 자원을 사용할 수 있습니다.
왜 선형 척도에서 샘플을 뽑는 것은 안 좋을까요?
만약 β가 1에 가깝다면, β가 아주 조금만 바뀌어도 결과가 아주 많이 바뀌게 됩니다. 예를 들어 β가 0.9에서 0.9005로 바뀌었다면 결과에 거의 영향을 주지 않습니다. 하지만 β가 0.999에서 0.9995로 바뀌었다면 알고리즘의 결과에 큰 영향을 줄 겁니다. 첫번째 경우는 대략 10개의 값을 평균내는 것이지만 두번째 경우는 마지막 1000개 값의 지수가중평균을 내는 것에서 마지막 2000개 값의 평균을 내는 것으로 바뀌었으니까요. 왜냐하면 1/(1-β)라는 식이 β가 1에 가까워질수록 작은 변화에도 민감하게 반응하기 때문입니다. 따라서 β가 1보다 가까운 곳에서 더 조밀하게 샘플을 뽑습니다. 반대로 1-β는 0이 가까운 곳이 되겠지요. 따라서 가능한 결과 공간을 탐색할 때 더 효율적으로 샘플을 추출할 수 있는 것입니다.
만약 하이퍼파라미터를 고를 때 적절한 척도를 사용하지 않더라도 크게 걱정할 필요는 없습니다. 다른 척도가 우선하는 상황에서 균일한 척도에서 샘플링을 하더라도 정밀화 접근을 사용하면 괜찮은 결과를 얻을 수 있을 테니까요. 그래서 반복할수록 더 유의미한 하이퍼파라미터 범위를 탐색하게 되는 것이죠.
3. 하이퍼파라미터 튜닝 실전

하이퍼파라미터 탐색 팁
오늘날 딥러닝은 여러 분야에 적용되고 있습니다. 한 어플케이션에서 얻은 하이퍼파라미터에 대한 직관이 다른 영역에서 쓰일 수도, 아닐 수도 있습니다. 서로 다른 어플리케이션 영역 간에 공유되는 것들이 있는데요. 예를 들면 컴퓨터 비전 커뮤니티에서 발전된 컨브넷이나 레스넷 등이 있는데요. 강의 뒷 부분에서 다시 다룰 겁니다. 이것들은 음성에 잘 적용되고 있죠. 그리고 이 음성에서 발전된 아이디어들이 자연어 처리에서도 잘 적용되고 있는 것을 봤습니다. 즉 딥러닝 분야의 사람들이 다른 영역에서 영감을 얻기 위해 그 분야의 논문을 점점 많이 찾아 읽고 있습니다.
하지만 하이퍼파라미터를 찾는 과정은 그렇지 못하다는 직관을 얻었습니다. 로지스틱 문제 하나만 보더라도 여러분이 좋은 하이어파라미터를 찾았다고 할 때 알고리즘을 계속 발전시키거나 몇 달에 걸쳐 데이터가 바뀔 수도 있고요. 데이터 센터의 서버를 업그레이드 시킬 수도 있겠죠. 이러한 변화들 때문에 여러분이 찾았던 하이퍼파라미터가 녹스는 겁니다. 그래서 다시 시험해보거나 하이퍼파라미터들이 아직도 만족할만한 결과를 내는지 몇 달마다 재평가하기를 권합니다.

결국 사람들이 하이퍼파라미터를 찾을 때 크게 두 가지 서로 다른 방법을 사용하는 것을 봤습니다.
하나는 모델 돌보기인데요. 데이터는 방대하지만 CPU나 GPU 등 컴퓨터 자원이 많이 필요하지 않아서 적은 숫자의 모델을 한번에 학습시킬 수 있을 때 사용합니다. 이런 경우에 학습 과정에서 모델 돌보기를 하는데요. 예를 들어 0일차에 무작위하게 매개변수를 설정하고 학습을 시작했습니다. 그러면 학습곡선에서 비용함수 J나 개발 세트의 오차가 하루가 다르게 점진적으로 감소할 겁니다. 그러면 1일차 끝 무렵에 학습이 꽤나 잘 되었네. 그럼 학습 속도를 조금 올려서 조금 더 나은지 보자고 말할 수 있겠죠. 이런 식으로 성능을 올려가는 겁니다. 그리고 2일차에도 꽤 좋은 성과를 내고 있는 것 같습니다. 여기서도 모멘텀을 약간 올리거나 학습 속도를 약간 낮출 수 있겠죠. 그리고 3일차에 들어섭니다. 커서 몇 일 전으로 돌아가기도 하겠죠. 이렇게 며칠, 몇 주에 걸쳐 매일 모델을 돌보며 학습시키는 겁니다. 모델 돌보기는 성능을 잘 지켜보다가 학습 속도를 조금씩 바꾸는 방식인 거죠. 이 방식은 여러 모델을 동시에 학습시킬 컴퓨터 자원이 충분치 않을 때 사용합니다.
다른 접근은 여러 모델을 함께 학습시키는 건데요. 여러분이 갖고 있는 하이퍼파라미터를 며칠에 걸쳐 스스로 학습하게 합니다. 그럼 이런 학습 곡선이 얻어지겠죠? 비용 함수 J를 그린 것일 수도 있고요. 학습 오차나 개발 세트의 오차 등 어떤 수치를 나타내고 있을 겁니다. 그리고 동시에 다른 모델의 다른 하이퍼파라미터 설정을 다루기 시작합니다. 두 번째 모델을 다른 학습 곡선을 그리겠지요? 그리고 동시에 세 번째 모델도 학습시킵니다. 학습 곡선이 이렇게 그려지고요. 또 다른 것은 이렇게 발산한다고 합시다. 이렇게 서로 다른 모델을 동시에 학습시키는 겁니다. 이 방법을 쓰면 여러 하이퍼파라미터 설정을 시험해볼 수 있죠. 그리고 마지막에는 최고 성능을 보이는 것을 고르는 겁니다.
Panda vs Caviar 비유를 하자면 왼쪽 접근은 판다 같습니다. 팬더는 한 번에 한 마리 씩만 아이를 갖죠. 그리고 아기 팬더가 살아남을 수 있도록 정말 많은 노력을 기울입니다. 말 그대로 모델이나 아기 팬더를 '돌보기'하는 거죠.
오른쪽 접근은 제가 캐비어 전략이라고 부르는데요 물고기랑 비슷하기 때문입니다. 한 철에 1억개의 알을 품는 물고기가 있는데요. 물고기가 번식을 하는 과정은 하나에 많은 집중을 쏟기보다 하나 또는 그 이상이 더 잘 살아남기를 바라며 그저 지켜보는 것입니다. 제가 생각컨대 이것은 포유류의 번식과 어류, 파충류의 번식의 차이인 것 같아요. 더 기억하기 쉽고 재밌으니 이제부터 판다 접근, 캐비어 접근이라고 부르겠습니다.
이 두 접근 중에 뭘 선택할지는 컴퓨터 자원의 양과 함수 관계에 있습니다. 만약 여러 모델을 동시에 학습시키기에 충분한 컴퓨터를 갖고 있다면 물론 캐비어 접근을 사용해서 서로 다른 하이퍼파라미터를 시험해볼 수 있겠죠. 하지만 온라인 광고나 컴퓨터 비전 어플리케이션 등 많은 데이터가 쓰이는 곳에서는 학습시키고자 하는 모델이 너무 커서 한 번에 여러 모델을 학습시키기 어렵습니다. 물론 어플리케이션에 따라 큰 차이가 있지만 팬더 접근을 주로 사용하더군요. 하나의 모델에 집중해 매개변수를 조금씩 조절하며 그 모델이 잘 작동하게끔 만드는 것이죠. 하지만 팬더 접근에서도 한 모델이 잘 작동하는지 확인한 뒤에 2주, 3주 후에 다른 모델을 초기화해서 다시 돌보기를 할 수 있습니다. 팬더가 일생에 여러 마리의 새끼를 돌보는 것처럼요. 한 번에는 하나 혹은 아주 적은 숫자의 새끼만 돌보지만 말이죠.
'Deep Learning > Basics' 카테고리의 다른 글
| [Andrew Ng] 딥러닝 2단계 : 7. 다중 클래스 분류 (2) | 2024.02.01 |
|---|---|
| [Andrew Ng] 딥러닝 2단계 : 6. 배치 정규화 (0) | 2024.02.01 |
| [Andrew Ng] 딥러닝 2단계 : 4. 최적화 알고리즘 (1) | 2024.01.29 |
| [Andrew Ng] 딥러닝 2단계 : 3. 최적화 문제 설정 (1) | 2024.01.25 |
| [Andrew Ng] 딥러닝 2단계 : 2. 신경망 네트워크의 정규화 (2) | 2024.01.25 |




