| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- LSTM
- RESNET
- 최단 경로
- 알고리즘
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 머신러닝
- 이진 탐색
- 선형대수
- AI
- 정렬
- 딥러닝
- DFS
- 그리디
- GRU
- Machine Learning
- 삽입정렬
- BFS
- pytorch
- 스택
- 퀵정렬
- 선택정렬
- 재귀함수
- 큐
- 계수정렬
- 인공지능
- rnn
- 다이나믹 프로그래밍
- Today
- Total
hyeonzzz's Tech Blog
[Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (1) 본문
1. 이진 분류
▶ 이진 분류 (Binary Classification)
: 그렇다 / 아니다 2개로 분류하는 것
입력된 사진을 나타내는 feature vector x를 가지고 y가 0인지 1인지를 예측하는 것 (‘그렇다’ = 1, ‘아니다’= 0 )

- 빨강, 초록, 파랑 픽셀을 한 열로 나열하면 벡터 x의 전체 차원은 64*64*3 = 12288이 된다
- 특성 벡터 x를 가지고 y가 1인지 0인지 예측한다
*신경망에서 학습하는 방법은 순전파 (forward propagation)와 역전파 (back propagation)가 있다
▶ 표기법 설명
- x : 훈련 샘플들
- y : 출력될 레이블
- m : 훈련샘플의 갯수
- 훈련 세트 : {(x^(1),y^(1)), (x^(2),y^(2)),..., (x^(m),y^(m))}
- m_train : train 세트의 갯수. m_test : test 세트의 갯수
- X : n_x * m 행렬

- X.shape -> 행렬의 차원을 알 수 있다
- Y : 1 * m 행렬

2. 로지스틱 회귀
▶ 로지스틱 회귀 (Logistic Regression)
: 주어진 입력 변수와 해당 입력 변수들에 따라 이진 분류 문제를 수행하는 데 사용되는 선형 모델
입력 변수의 선형 결합을 로지스틱 함수에 통과시켜서 각 클래스에 속할 확률을 예측한다.
▶ 변수 설명
X : 입력 특성
y : 주어진 입력특성 X에 해당하는 실제 값
ŷ: 입력 특성 x가 주어졌을 때 y가 1일 확률 ( 0 ≤ ŷ ≤ 1 )
(사진이 고양이 사진일 확률)
▶ 선형 회귀

원래는 위의 식을 통해 계산하지만, 0 ≤ ŷ ≤ 1 이어야 한다
따라서 sigmoid 함수를 적용해 다음 식으로 변형한다
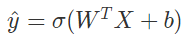
▶ Sigmoid 함수 (= 로지스틱 함수)


-> z가 무한대일때 1에 가까워진다
-> z가 음수일수록 0에 가까워진다
로지스틱 회귀를 구현할 때 y가 1일 확률을 잘 예측하도록 파라미터 w와 b를 학습해야 한다
3. 로지스틱 회귀의 비용함수

위첨자 (i)는 i번째 훈련 샘플에 관한 데이터임을 뜻한다
매개변수들 w와 b를 학습하려면 비용함수를 정의해야 한다
▶ 손실 함수 (Loss Function)
: 훈련 샘플 하나에 대한 y(실제값)과 ŷ(예측값)의 오차를 계산

원래는 이 식을 사용하지만 로지스틱 회귀에서는 지역 최솟값에 빠질 수 있기 때문에 사용하지 않는다

1) y = 1 인 경우 손실값을 줄이려면 -> L(ŷŷ,y)= −logŷ 가 작아지도록 ŷŷŷŷ는 1에 수렴하도록 한다
2) y = 0 인 경우 손실값을 줄이려면 -> L(ŷŷ,y) = −log(1−ŷŷ) 가 작아지도록 ŷŷŷ 는 0에 수렴하도록 한다
▶ 비용 함수 (Cost Function)
: 훈련 샘플 전체에 대한 오차를 계산

전체 데이터셋의 예측이 얼마나 잘 평가되었는지 보여준다
* 로지스틱 회귀 모델을 학습하는 것 = cost function J를 최소화하는 매개변수 w, b를 찾는 것
* 로지스틱 회귀는 작은 신경망과 같다
4. 경사하강법
▶ 경사하강법 (Gradient Descent)
: cost function J를 최소화하는 파라미터 w와 b를 찾아내는 방법
함수의 기울기(경사)를 사용하여 함수의 최솟값을 찾아가는 최적화 알고리즘
주어진 함수의 기울기(경사)가 현재 위치에서 가장 크게 감소하는 방향으로 이동하여 함수의 최솟값을 찾는다. 이 과정을 반복하여 최솟값에 점점 더 가까워진다.

- J(w,b)는 w, b 위의 곡면
- 곡면의 높이 = J(w,b)의 값
- cost Function J는 볼록한 형태여야 한다 -> 지역 최적값이 1개이다
▶ 경사하강법을 이용해 J의 최솟값에 해당하는 w와 b를 찾는 방법
- w, b값을 한 값으로 초기화한다 (보통 0으로 설정)
- 초기점에서 가장 가파른 내리막 방향으로 한 단계 내려간다
- 반복하면 최적값에 도달한다

▶ Gradient Descent
:= 는 값을 갱신한다는 뜻

- α : learning rate (경사하강법을 반복할 때 한 단계의 크기를 결정한다)
- dJ(w)/dw : 도함수 (dw로 표기하기도 한다)

dw >0 이면, 파라미터 w 는 기존의 w 값 보다 작은 방향으로 업데이트되고,
dw <0 이면, 파라미터 w 는 기본의 w 값 보다 큰 방향으로 업데이트된다
-> 왼쪽에서 초기화하던 오른쪽에서 초기화하던 전역 최소값에 도달하게 된다!
* 변수가 2개 이상이면 편미분 기호를 이용 (소문자 d와 의미 거의 동일)

☆ 세션 진행 후 추가 내용
Q. 왜 손실 함수 (loss function) 에 MSE대신 더 복잡한 함수를 사용하는가?
보통 손실 함수는

식을 사용하지만 로지스틱 회귀에서 이 식을 사용하면 지역 최솟값에 빠질 수 있기 때문에 사용하지 않는다
볼록한 형태가 아니라 울퉁불퉁한 형태가 나와 최솟값을 구할 수 없게 된다
※참고자료
https://copycode.tistory.com/162
머신러닝(Machin Learning) 6장 - Logistic Regression 의 cost function -
머신러닝(Machin Learning) 6장- Logistic Regression 의 cost function - Cost function은 예측을 하는 값과 실제 결과 값의 차이를 나타내는 함수이다. 예측을 하는 데이터를 바꾸어가면서 실제 결과 값과 차이를
copycode.tistory.com
'Deep Learning > Basics' 카테고리의 다른 글
| [Andrew Ng] 딥러닝 1단계 : 4. 얕은 신경망 네트워크 -(1) (0) | 2024.01.17 |
|---|---|
| [Andrew Ng] 딥러닝 2단계 : 1. 머신러닝 어플리케이션 설정하기 (0) | 2023.10.10 |
| [Andrew Ng] 딥러닝 1단계 : 3. 파이썬과 벡터화 (0) | 2023.09.19 |
| [Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (2) (0) | 2023.09.12 |
| [Andrew Ng] 딥러닝 1단계 : 1. 딥러닝 소개 (0) | 2023.09.12 |




