Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 선형대수
- pytorch
- 최단 경로
- 다이나믹 프로그래밍
- 선택정렬
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 삽입정렬
- 계수정렬
- RESNET
- 이진 탐색
- DFS
- 알고리즘
- 재귀함수
- BFS
- rnn
- 정렬
- 딥러닝
- AI
- 스택
- GRU
- 큐
- 인공지능
- 머신러닝
- LSTM
- Machine Learning
- 퀵정렬
- 그리디
Archives
- Today
- Total
hyeonzzz's Tech Blog
[Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (2) 본문
1. 계산 그래프 (Computation Graph)
▶ 계산 그래프 (Computation Graph)
: 계산 과정을 그래프로 나타낸 것
▶ 신경망의 계산
- 순전파 (forward propagation) : 신경망의 출력값을 계산
- 역전파 (back propagation) : 경사나 도함수를 계산
▶ J(a,b,c)=3(a+bc) 의 계산 그래프 만드는 과정

- u = bc
- v = a+u
- J = 3v

2. 계산 그래프로 미분하기
▶ 연쇄 법칙 (Chain rule)
: 합성함수의 도함수는 합성함수를 구성하는 함수의 미분을 곱함으로써 구할 수 있다

▶ back propagation 이용
1. v에 대한 J의 도함수 구하기
v = 11 -> 11.001
J = 33 -> 33.003
따라서 v에 대한 J의 도함수는 3이다
2. a에 대한 J의 도함수 구하기
a = 5 -> 5.001
v = 11 -> 11.001
J = 33 -> 33.003
따라서 a에 대한 J의 도함수는 3이다
* a를 바꾸면 -> v가 증가 -> J가 증가

3. u에 대한 J의 도함수 구하기
u = 6 -> 6.001
v = 11 -> 11.001
J = 33 -> 33.003
따라서 u에 대한 J의 도함수는 3이다

4. b에 대한 J의 도함수 구하기

v에 대한 도함수를 구함 -> a에 대한 도함수를 구함 -> u에 대한 도함수를 구함 -> b와 c에 대한 도함수를 구함 (연쇄 법칙)
* 코드 작성시 표기법

빨간색 화살표 방향으로 연쇄법칙을 이용해 derivatives 구한다

3. 로지스틱 회귀의 경사하강법
▶ 로지스틱 회귀의 구현


1. 입력값 x1, x2가 들어간다
2. 가중치 w1, w2 편향 b를 선형 결합해 z를 계산한다
3. z에 활성화 함수를 적용한다 -> y=1일 확률 a가 나온다
4. a에 임계함수를 적용해 0,1로 분류한다
▶ 로지스틱 회귀의 경사하강법 한 단계
- 경사하강법 : 손실 함수의 값이 최소가 되는 지점을 찾아가는 방법
- 로지스틱 회귀에서의 목적 : 매개변수 w와 b를 변경해서 손실을 줄인다
- 구하고자 하는 것 : 손실 함수의 도함수
1. da 구하기


2. dz 구하기


3. dw1, dw2, db 구하기


4. w1, w2, b 구하기
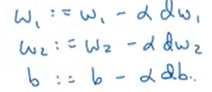
지금까지는 단일 샘플에 대한 경사하강법을 계산했다. 아래부터는 m개 샘플에 대한 경사하강법이다
4. m개 샘플의 경사하강법
▶ 로지스틱 회귀에서 비용 함수(cost function)


▶ 프로그래밍

- m개의 훈련 샘플 반복 + n개 특성 반복 (2개 for문)
- 이중 for문이 포함되어 있다 -> 계산 속도가 느리다
- 벡터화 (vectorization) 를 이용하면 for문을 사용하지 않고 처리할 수 있다
'Deep Learning > Basics' 카테고리의 다른 글
| [Andrew Ng] 딥러닝 1단계 : 4. 얕은 신경망 네트워크 -(1) (0) | 2024.01.17 |
|---|---|
| [Andrew Ng] 딥러닝 2단계 : 1. 머신러닝 어플리케이션 설정하기 (0) | 2023.10.10 |
| [Andrew Ng] 딥러닝 1단계 : 3. 파이썬과 벡터화 (0) | 2023.09.19 |
| [Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (1) (0) | 2023.09.12 |
| [Andrew Ng] 딥러닝 1단계 : 1. 딥러닝 소개 (0) | 2023.09.12 |




