| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 알고리즘
- 선택정렬
- 퀵정렬
- AI
- DFS
- 큐
- 정렬
- RESNET
- 인공지능
- 선형대수
- 그리디
- 딥러닝
- 최단 경로
- 이진 탐색
- Machine Learning
- 캐치카페신촌점 #캐치카페 #카페대관 #대학생 #진학사 #취준생
- 스택
- GRU
- 다이나믹 프로그래밍
- 계수정렬
- rnn
- 재귀함수
- BFS
- LSTM
- 머신러닝
- pytorch
- 삽입정렬
- Today
- Total
hyeonzzz's Tech Blog
[Andrew Ng] 딥러닝 1단계 : 3. 파이썬과 벡터화 본문
1. 벡터화
▶ 벡터화 (Vectorization)
- 내장 함수를 써 코드에서 for문을 없앨 수 있다
- 큰 데이터 세트를 학습시킬때 코드 실행시간을 줄일 수 있어 중요하다
▶ 로지스틱 회귀 계산 - Non-vectorized

w, x : 열 벡터 (R^(n_x)의 차원을 가진 벡터)
벡터화 되지 않은 구현일 땐 w^Tx를 계산하기 위해
z=0
for i in range(n_x):
z+= w[i] * x[i]
z += b를 계산해야 했다. 벡터화되지 않아 느리다
▶ 로지스틱 회귀 계산 - Vectorized
w^Tx 를 직접 계산한다
z = np.dot(w,x) + b훨씬 빠르다
▶ 코드 실습
import numpy as np
a = np.array([1,2,3,4])
print a[ 1 2 3 4 ]
#벡터화 이용
import time
a = np.random.rand (1000000) #난수로 이루어진 백만 차원의 배열 생성
b = np.random.rand (1000000)
tic = time.time() //현재 시간으로 설정
c = np.dot(a,b)
toc = time.time()
print(c)
print(“Vectorized version:” + str(1000*(toc-tic)) + “ms”)→ 평균적으로 1.5~3.5밀리초가 걸린다
#벡터화 이용X
c = 0
tic = time.time()
for i in range(1000000):
c += a[i] * b[i]
toc = time.time()
print(c)
print(“for loop:” + str(100*(toc-tic)) + “ms”)→ 평균적으로 500밀리초가 걸린다 (약 300배)
* 벡터화를 이용하면 빠른 연산이 가능하다!!
▶ SIMD (Single Instruction Multiple Data)
: 병렬 프로세서의 한 종류로, 하나의 명령어로 여러 개의 값을 동시에 계산하는 방식
- gpu와 cpu에게 simd라고 불리는 병렬 명령어가 있다
- np.dot을 사용하거나 for문이 필요 없는 다른 함수를 사용할 때, 파이썬 numpy가 병렬화의 장점을 통해 계산을 훨씬 빠르게 할 수 있게 해준다 (cpu와 gpu상의 계산에서 모두 적용되는 이야기)
2. 더 많은 벡터화 예제
가능한 한 for문을 쓰지 말아야 한다!
▶ 예1) u = Av
1. 벡터화 사용하지 않는 경우 - 두개의 for문을 사용한다

2. 벡터화 사용하는 경우 - u = np.dot(A,v)

▶ 예2) 벡터v의 모든 원소에 지수 연산

1. 벡터화 사용하지 않는 경우
u = np.zeros((n,1)) #u를 0인 벡터로 초기화
for i in range(n) :
u[i] = math.exp(v[i])
2. 벡터화 사용하는 경우 - 훨씬 빠르다
import numpy as np
u = np.exp(v)▶ 다른 numpy 라이브러리들 (내장 함수들)
- np.log(v) //원소의 로그값
- np.abs(v) //절대값
- np.max(v,0) //v의 원소와 0중에서 더 큰 값 반환
- v**2 //모든 원소를 제곱한 벡터를 반환
- 1/v //원소의 역수로 이루어진 벡터를 반환
▶ 로지스틱 회귀와 경사 하강법에 벡터화 적용하기

- m개의 훈련 샘플 반복 + n개 특성 반복 (2개 for문)
- 이중 for문이 포함되어 있다 -> 계산 속도가 느리다
- 벡터화 (vectorization) 를 이용하면 for문을 사용하지 않고 처리할 수 있다
벡터화를 이용해 두번째 for문을 제거한다
원래 코드

for문을 제거한 코드
dw를 벡터화한다!!

- dw = np.zeros((n_x,1))
- dw += x(i)dz(i)
- dw /= m
* 두번째 for문을 dw += x^(i)dz^(i) 로 대체하였다!!
3. 로지스틱 회귀의 벡터화 - 전방향 전파
: 벡터화를 이용해 for문이 하나도 없는 신경망으로 만들 수 있다
▶ 전방향 전파
z^(i)=W^T*x^(i)+b
a^(i)=σ(z^^(i))
→ m개의 훈련 샘플이 있다면 m번 반복해야 한다
▶ X : 훈련 입력을 열로 쌓은 행렬 ((n_x, m)차원 행렬)

소문자 x를 가로로 쌓아서 대문자 X를 얻는다
소문자 z와 a를 하나씩 계산하기 위해 m개의 훈련 샘플을 순환하는 대신
한 줄의 코드로 모든 z를 동시에 계산할 수 있다
또한 적절한 시그마의 구현으로 한줄의 코드로 모든 a를 동시에 계산할 수 있다
▶ z^(1), z^(2), z^(3) 한 줄의 코드로 계산하기
(1,m) 행렬 만들기

Z = np.dot(w.T,X) + b*b는 (1,1) 실수이지만 파이썬이 자동으로 (1,m) 벡터로 바꿔준다
→ Broadcasting
▶ a^(1)부터 a^(m)을 동시에 계산하기

소문자 a를 가로로 쌓아 대문자 A를 얻는다
sigmoid 함수가 대문자 Z를 입력으로 받고 대문자 A를 반환한다
4. 로지스틱 회귀의 경사 계산을 벡터화 하기 - 역전파
: 벡터화를 통해 m개의 전체 훈련 샘플에 대한 경사 계산을 동시에 한다
▶ dZ 정의하기
dz^(i)=a^(i)−y^^^(i)



▶ 남아있는 for문
지난 구현에서 훈련 샘플을 계산하는 for문은 여전히 남아있었다
dw = 0으로 초기화한 후 여전히 훈련 샘플을 순환해줘야 했다
▶ db 계산하기
db는 모든 dz를 더하고 m으로 나눠주어 계산한다


db = (1/m)np.sum(dZ)
▶ dw 계산하기


dw = (1/m)Xdz^T
▶ 모든 것 모아 로지스틱 회귀 구현하기
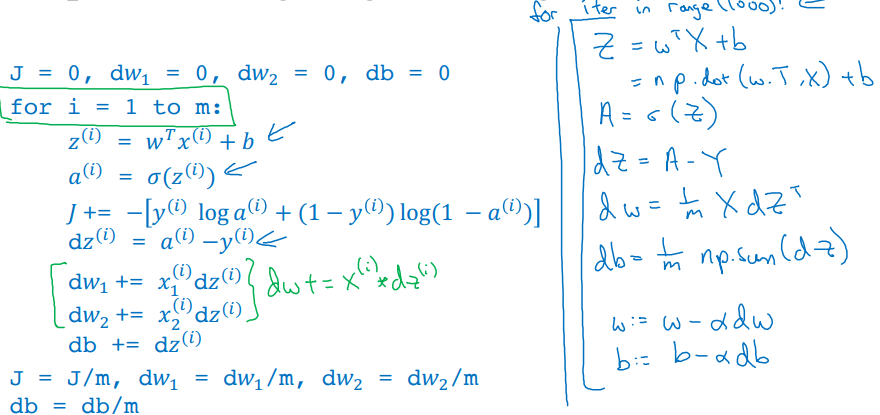
→ 로지스틱 회귀 경사 하강법의 한 반복 구현
경사하강법을 여러번 반복하고싶다면 가장 바깥쪽의 for문은 없앨 방법은 없다...
전방향 전파, 역방향 전파, m개의 훈련 샘플에 대한 예측값과 도함수 계산 완료!!
5. 파이썬의 브로드캐스팅
▶ Broadcasting
: 일정 조건을 부합하는 다른 형태의 배열끼리 연산을 수행하는 것
파이썬 코드 실행 시간을 줄일 수 있다
▶ 예 1)
▷ 네 가지 음식의 carb, protein, fat의 칼로리의 백분율 구하기

- Apples의 열 모두 더하면 -> 100g의 사과는 59 칼로리를 가지고 있다
- 사과에서 탄수화물이 주는 칼로리의 백분율 = 56/59 (약 94.9%)
▷ 행렬의 네 열 안의 수의 합을 구하고 행렬 전체를 나눠서 백분율을 구한다 - for문 없이!
- A 행렬 - (3,4) 행렬
- 각 열의 합을 구한다
- 각 네 열을 각 열의 합으로 나눈다
▷ 파이썬 코드
- 배열 정의
import numpy as np
A = np.array([[56.0, 0.0, 4.4, 68.0],
[1.2, 104.0, 52.0, 8.0],
[1.8, 135.0, 99.0, 0.9]])
print(A)
- 열 더하기
cal = A.sum(axis=0) #열을 더한다. axis=1이면 가로로 더한다
print(cal)[ 59, 239, 155.4, 76.9]
- 백분율 구하기
# (3,4) 행렬인 A를 (1,4) 행렬로 나눈다
# 사실 코드 첫 줄이 실행된 이후에 cal은 이미 (1,4) 행렬이다
# reshape 함수를 사용할 필요가 없다
percentage = 100*A/cal.reshape(1,4) # 하지만 reshape를 이용해 행렬의 차원을 확실시할 수 있다
print(percentage)db = (1/m)np.sum(dZ)db = (1/m)np.sum(dZ)db = (1/m)np.sum(dZ)db = (1/m)np.sum(dZ)db = (1/m)np.sum(dZ)db = (1/m)np.sum(d
100*A/cal.reshape(1,4)
- 파이썬 브로드캐스팅의 한 예시
- (3,4) 행렬인 A를 (1,4) 행렬로 나눈다
▶ 예 2)
▷ (4,1) 벡터에 상수 더하기

파이썬이 상수를 자동으로 (4,1) 벡터로 바꿔준다
▶ 예 3)
▷ (2,3) 행에 (1,n) 행렬 더하기

파이썬이 (1,n) 행렬을 자동으로 (m,n) 행렬로 바꿔준다
▶ Broadcasting 원리
(m,n) 행렬에 (1,n) 행렬을 더하거나 빼거나 곱하거나 나눈다면
(1,n) 행렬을 m번 복사해서 (m,n) 행렬로 만든 뒤
요소별 연산을 해준다
(m,n) 행렬에 (m,1) 행렬을 더하거나 빼거나 곱하거나 나눈다면
(m,1) 행렬을 n번 복사해서 (m,n) 행렬로 만든 뒤
요소별 연산을 해준다
6. 파이썬과 넘파이 벡터
: 파이썬의 넘파이 패키지에 대해서 주의할 점
▷ 예) 가우시안 분포를 따르는 변숫값 5개를 배열 a에 저장
import numpy as np
a = np.random.randn(5) # 표준정규분포를 따르는 변숫값 5개를 배열 a에 저장print(a)
print(a.shape) #(5,) -> 랭크가 1인 배열, 행 벡터도 아니고 열 벡터도 아니다
print(a.T) #전치를 했지만 a와 출력 결과가 같다
print(np.dot(a,a.T)) #a와 a전치의 내적을 구하면 하나의 수만 나온다a.shape = (n,)
- rank 1 array
- 행 벡터도 열 벡터도 아니다
- 결과가 직관적이지 않다
- 사용하지 않는 것이 좋다!!
a = np.random.randn(5,1)
print(a)
print(a.T) #행 벡터가 된다, [[]] 형태, 사실 1*5 행렬
print(np.dot(a,a.T)) #벡터의 외적이 나온다(행렬)a = np.random.randn(5,1)
→ (5,1) 열 벡터로 만들거나
a = np.random.randn(1,5)
→ (1,5) 행 벡터로 만드는 것이 좋다
+ assert(a.shape == (5,1)) 사용하기
a가 (5,1) 열 벡터라는 걸 확실히 하기 위해 사용한다
+ a = a.reshape((5,1)) 사용하기
reshape 함수를 써서 (5,1) 배열이나 (1,5) 배열로 바꾸어 동작하게 한다
7. 로지스틱 회귀의 비용함수 설명
▶ 로지스틱 회귀의 손실함수

- y값이 1 이 될 확률 : P(y=1∣x) = ŷŷ
- y값이 0 이 될 확률 : P(y=0∣x) =1 −ŷ ŷ
두 경우를 하나의 수식으로 나타내면 다음과 같다

- 만약에 y = 1 일 경우, P(y∣x) = ŷ^1(1−ŷŷ)^0 =ŷ ŷ
- 만약에 y = 0 일 경우, P(y∣x) = ŷ^ŷ 0(1−ŷŷ)^1 = 1−ŷ
로그함수가 강한 단조 증가 함수이기 때문에 위 식은 아래의 식과 동일하다
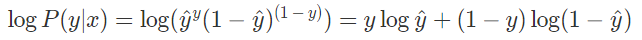
우리의 목적은 확률( logP(y∣x) )을 최대화 시키는 것이기 때문에 이와 등치인 -1 을 곱한 확률 ( −logP(y∣x) )를 최소화를 목적으로 손실함수를 정의한다
▷ 훈련 샘플 하나의 손실함수

손실함수를 최소화 = 확률의 로그값을 최대화
▷ 전체 훈련 샘플의 비용함수
훈련 샘플들이 독립동일분포라고 가정하면, 전체 샘플에 대한 확률은 각 확률의 곱이다



비용함수는 손실함수들의 평균을 최소화하는 것으로 정의!
☆ 세션 진행 후 추가 내용
Q1. 브로드캐스팅이 가능한 경우?
1. (3,1) (1,3) 처럼 차원의 짝이 맞을 때
2. (4,4) (1,4) 처럼 하나의 배열의 차원이 1일 때
3. (4,4) 1 처럼 멤버가 하나인 배열일 때
*참고자료 : https://appia.tistory.com/184
파이썬[Python] numpy 브로드캐스팅(Broadcasting)정의 및 조건
Numpy에서 브로드캐스팅(Broadcasting)이라는 단어를 매우 많이 사용합니다. 실제로 이 단어는 통신에서는 주변에 모든에게 패킷을 뿌리는 그런 느낌이었습니다. (물론 살짝 어감의 차이는 있을 수
appia.tistory.com
Q2. rank가 1이라는게 정확히 무슨 의미인가?
좌에서 우로 또는 위에서 아래로 나열되어 있는 형태가 아니기 때문에 행벡터도 열벡터도 아니다
Q3. 다음 중 뉴런이 계산하는 것은 무엇인가?
1. 활성화 함수를 계산한 후 선형함수(z = Wx+b) 계산
2. 출력값을 활성화 함수에 적용하기 전 모든 feature의 평균 계산
3. 입력 x를 선형적으로 확장하는 함수 g (Wx+b) 계산
4. 선형함수(z = Wx+b)를 계산한 후 활성화 함수→ 뉴런은 입력값 x에 가중치 행렬 W와 편향 벡터 b를 적용하여 선형 함수 z = Wx+b를 계산한 다음, 이 선형 함수의 결과를 활성화 함수에 적용하여 최종 출력을 생성한다
→ 로지스틱 회귀에서의 활성화 함수는 sigmoid 함수이다
Q4. print(d[1,1:3])의미?
d행렬의 두번째 행의 두번째 열부터 세번째 열까지 출력한다
Q5. np.random 차이
np.random.rand(100) : 0과 1 사이의 랜덤한 부동소수점 숫자 100개를 생성한다
np.random.randn(100) : 표준 정규 분포를 따르는 랜덤한 부동소수점 숫자 100개를 생성한다
np.random.randint(100) : 0 이상 99 이하의 랜덤한 정수 하나를 생성한다
Q6. 비용함수에서 log를 사용하는 이유?
매끈한 경사를 만들기 위해 log를 사용한다
*참고자료 : https://mobicon.tistory.com/544
[Cost Function] 로지스틱 회귀의 비용함수 이해
텐서플로우 강좌를 들으면서 다음의 모델을 실습으로 쥬피터에 코딩을 했다. 여기서 Cost function을 짤때 log함수를 왜 사용하고 앞에 - (마이너스)값은 왜 붙이는지 정리해 본다. 준비 - 아나콘다
mobicon.tistory.com
db = (1/m)np.sum(dZ)(1,m) 행렬ㅇㅇ
'Deep Learning > Basics' 카테고리의 다른 글
| [Andrew Ng] 딥러닝 1단계 : 4. 얕은 신경망 네트워크 -(1) (0) | 2024.01.17 |
|---|---|
| [Andrew Ng] 딥러닝 2단계 : 1. 머신러닝 어플리케이션 설정하기 (0) | 2023.10.10 |
| [Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (2) (0) | 2023.09.12 |
| [Andrew Ng] 딥러닝 1단계 : 2. 신경망과 로지스틱회귀 (1) (0) | 2023.09.12 |
| [Andrew Ng] 딥러닝 1단계 : 1. 딥러닝 소개 (0) | 2023.09.12 |




